Элементы тригонометрии и Офисные информационные технологии

Введение вспомогательного угла

Рассмотрим уравнение вида:  a sin x + b cos x = c , где  a, b, c – коэффициенты;  x – неизвестное.

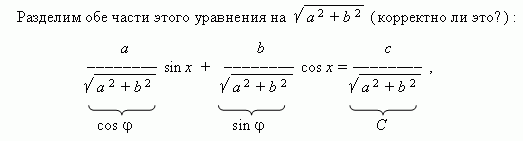
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos и sin ( здесь - так называемый вспомогательный угол ), и наше уравнение принимает вид:

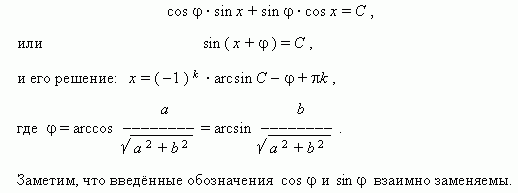
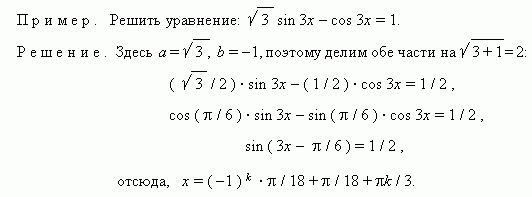
   Способ подстановки

Пример 1. 2 sin²x = 3cosx.

Решение. 2sin²x - 3cosx = 0; 2 (l - cos²x) - 3cosx = 0; 2cos²x + 3cosx - 2 = 0.

Пусть z = cosx, тогда 2z² + 32z - 2=0.

Д = 9+16 = 25;  = 5;  z1 = (-3 + 5)/4 = 1/2; z2 = (-3-5)/ 4 = -2 – не удовлетво­ряют

условию для z. Тогда решим одно простейшее уравнение:

cosx = 1/2; х = ± п/3 + 2пn, . Ответ: х = ± п/3 + 2пn, .

 Универсальная подстановка

 Рассмотрим этот метод на примере.

П р и м е р .   Решить уравнение:  3 sin x – 4 cos x = 3 .

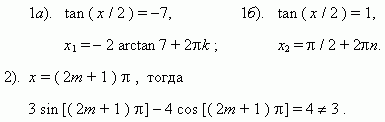
   Таким образом, решение даёт только первый случай.