Лекция №3. Уравнение вида a sinx + b cosx = с. Уравнения, рациональные относительно выражений sin x+cos x и sin x*cos x. Тригонометрические уравнения, приводимые к квадратному
![]() Уравнение вида a sinx + b cosx = с
Уравнение вида a sinx + b cosx = с
Пусть ![]() разделим обе его части на
разделим обе его части на ![]() , тогда
, тогда ![]()
Пусть – одно из решений системы 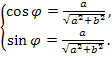
Воспользовавшись этими равенствами, запишем уравнение в виде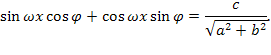
Применив формулу ![]() получим уравнение
получим уравнение ![]() которое, как видно равносильно исходному уравнению. Если
которое, как видно равносильно исходному уравнению. Если ![]() то уравнение имеет решение
то уравнение имеет решение ![]() или
или ![]() Если
Если ![]() то уравнение решений не имеет.
то уравнение решений не имеет.
Пример . 3sinx + 4cosx = 5.
Решение. Разделим обе части уравнения на 5, тогда (3/5)sin x+(4/5) cos x=1
sin j = 4/5; cos j = 3/5; sin ( x+ j ) = 1, x + j = п / 2 + 2 п n, n Î Z .
Ответ: x = п/ 2 - arcsin + 2 п n , n Î Z .
Уравнения, рациональные относительно выражений sin x+cos x и sin x cos x
Если левая часть тригонометрического уравнения f=0 содержит лишь одно из выражений sin x+cos x или sin x - cos x и функцию sin 2x (или произведение sin x cos x ) то, вводя новое неизвестное t=sin x + cos x или t=sin x - cos x и учитывая, что sin 2x=(sin x+cos x)2-1, 2x=1-(sin x-cos x)2 , приходим к уравнению относительно t .
Пример. ![]()
Решение. Понижая степень ![]() , получаем
, получаем ![]() или
или ![]() сделаем замену
сделаем замену ![]() тогда
тогда ![]() Тем самым исходное уравнение приводится к квадратному относительно t уравнению:
Тем самым исходное уравнение приводится к квадратному относительно t уравнению: ![]() откуда
откуда ![]() Находим
Находим ![]()
Ответ: ![]()
Тригонометрические уравнения, приводимые к квадратному
Заметим, что если тригонометрическое уравнение целого вида содержит только синусы или косинусы, то область допустимых значений переменной – множество действительных чисел, так как эти функции определены для любого действительного значения. Поэтому в дальнейшем при рассмотрении таких уравнений, как ![]()
область допустимых значений переменной не устанавливается.
Справедливы соотношения:
a) ![]()
b) ![]()
Формулы корней уравнений:
a) ![]()
b) ![]()
c) ![]()
Пример. ![]()
Решение. Пусть sinx=y, тогда уравнение можно записать в виде 8y2-6y-5=0.
Решая это уравнение, мы находим:![]() Следовательно
Следовательно ![]() или
или ![]() Решим уравнение
Решим уравнение ![]()
![]()
Уравнение ![]() корней не имеет, т.к. sin x не может быть больше единицы.
корней не имеет, т.к. sin x не может быть больше единицы.
Ответ: ![]()