Лекция №1. Простейшие тригонометрические уравнения
Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим.
Простейшие тригонометрические уравнения:
Простейшими тригонометрическими уравнениями называются уравнения вида:
![]()
![]()
![]()
![]()
где а – любое действительное число.
Решить простейшее тригонометрическое уравнение – значит найти множество всех углов (дуг), имеющих данное значение тригонометрической функции.
Рассмотрим решение простейших тригонометрических уравнений.
1. Sin x = a
|
a) Если |
|
|
b) Если |
|
|
c) Если |
|
|
d) |
|
|
e) Часто эти решения объединяют в одну формулу |
|
|
f) Формула для корней уравнения |
|
2. Cos x=a
|
a) Если |
|
|
b) Если |
|
|
c) Если |
|
|
d) |
|
|
e) |
|
|
f) Формулы для корней уравнения |
|
3. Tg x=a.
|
a) Если |
|
b) ![]()
c) ![]()
d) ![]()
e) Формула для корней уравнения ![]() имеет вид:
имеет вид: ![]()
4. Ctg x=a.
|
a)
|
|
|
b)
|
|
|
c)
|
|
|
d)
|
|
Тригонометрические уравнения вида ![]()
![]() - линейная функция,
- линейная функция, ![]() любые действительные числа, также относятся к простейшим уравнениям.
любые действительные числа, также относятся к простейшим уравнениям.
Пример 1. Решить уравнение ![]() .
.
Решение. Данное уравнение является однородным относительно ![]() и
и ![]() . Рассмотрим такие x, что
. Рассмотрим такие x, что ![]()
![]()
![]() для любых x. Следовательно,
для любых x. Следовательно, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Ответ: ![]()
Пример 2. ![]()
Решение. Решим уравнение относительно ![]()
![]() , отсюда по формуле решения уравнения sinx = а находим
, отсюда по формуле решения уравнения sinx = а находим 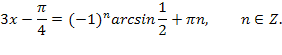
![]()
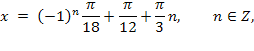
Если k = 2n (четное), то ![]()
Если k = 2n + 1 (нечетное число), то ![]()
Ответ: ![]()
или в градусах: х = 25° + 120· n, nÎZ; x = 65° + 120°· n, nÎZ.
Пример 3. ![]()
Решение. Подставим вместо ![]() значение
значение ![]() , тогда уравнение примет вид
, тогда уравнение примет вид 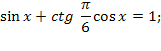
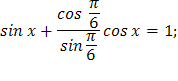
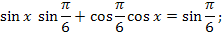
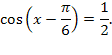
По формуле для уравнения ![]()
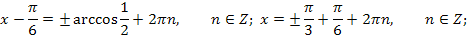
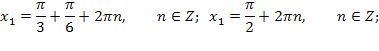
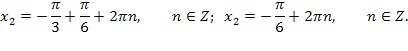
Ответ: ![]()