Лекция№2.Тригонометрические уравнения, содержащие тригонометрические функции одинакового аргумента. Однородные уравнения
Тригонометрические уравнения, содержащие тригонометрические функции одинакового аргумента
Рассмотрим тригонометрические уравнения, рациональные относительно тригонометрических функций.
Т.к. все тригонометрические функции рационально выражаются через sinx и cosx, то в общем случае рациональное уравнение относительно тригонометрических функций одного аргумента можно представить в виде
![]()
Где R – рациональная функция относительно sinx и cosx.
Если ![]() то любое тригонометрическое уравнение вида (1), рационально относительно всех входящих в него тригонометрических функций, можно привести к рациональному уравнению относительно неизвестного
то любое тригонометрическое уравнение вида (1), рационально относительно всех входящих в него тригонометрических функций, можно привести к рациональному уравнению относительно неизвестного ![]() с помощью формул, выражающих тригонометрические функции через тангенс половинного аргумента. Однако, решая уравнение таким методом, можно потерять корни вида
с помощью формул, выражающих тригонометрические функции через тангенс половинного аргумента. Однако, решая уравнение таким методом, можно потерять корни вида ![]()
![]() не имеет смысла. Поэтому необходимо проверять, являются ли числа
не имеет смысла. Поэтому необходимо проверять, являются ли числа
![]()
корнями исходного уравнения.
Если уравнение вида (1) или приводимое к нему при замене ![]() не изменяется, то его имеет смысл приводить к рациональному относительно sinx.
не изменяется, то его имеет смысл приводить к рациональному относительно sinx.
Если уравнение (1) или приводимое к нему не изменяется при замене ![]()
Если уравнение (1) или приводимое к нему при замене
Решение. Разделим обе части уравнения на 5, тогда 3/5sinx + 4/5cosx = 1.
sinj = 4/5; cosj = 3/5; sin(x+j) = 1, x + j = p/2 + 2pn, nÎZ.
Ответ: x = p/2 - arcsin 4/5 + 2pn, nÎZ.
Пример 2. ![]() (*)
(*)
Решение. Применим формулы 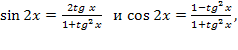 представим заданное уравнение в виде
представим заданное уравнение в виде 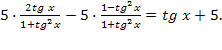
Уравнения (*) и (**) равносильны.
Пусть ![]()
![]()
Т.о. исходное уравнение (*) равносильно совокупности трех уравнений ![]()
которые имеют соответственно решения ![]()
![]()
Ответ: ![]()
Однородные тригонометрические уравнения имеют такой вид:
a sin2x + b sinxcosx + c cos2x = 0 (однородное уравнение 2-й степени) или
a sin3x + b sin2x cosx + c sinx cos2x + d sin3x = 0 (однородное уравнение 3-й степени) и т.д.
Общий вид однородного тригонометрического уравнения:
![]() .
.
В этих уравнениях sinx ¹ 0, cosx ¹ 0. Решаются они делением обеих частей уравнения на sinnx или на cosnx и приводятся к уравнениям относительно tgx или ctgx:
![]()
или
![]()
Справедливы соотношения:
4)
5)
Уравнение вида a
Уравнение вида ![]()
![]()
Уравнение вида ![]()
Называется однородным уравнением второй степени относительно ![]()
![]() тогдаполучим:
тогдаполучим:
![]()
Уравнение (2) равносильно уравнению (1), т.к. корни уравнения cos2 f(x)=0
Однако если a=0, то уравнение (1) принимает вид ![]() которое решается разложением левой части на множетели:
которое решается разложением левой части на множетели:
![]()
Пример. ![]()
Решение. Разложим sin4x по формуле синуса двойного угла.
Получим уравнение ![]()
Разделим на cos22x. Уравнение примет вид ![]()
Пусть z = tg2x, тогда ![]()
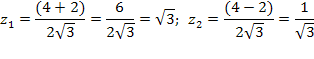

2x = p/3 + pn, nÎZ; 2x = p/6 + pn, nÎZ;
x1 = p/6 + pn/2, nÎZ ; x2 = p/12 + pn/2, nÎz.
Ответ: x1 = p/6 + pn/2, nÎZ ; x2 = p/12 + pn/2, nÎz.