Учебная практика

            Рассмотрим нелинейное дифференциальное уравнение x'(t)=f(t,x(t)),   (2.21) где f : R²→R — непрерывная 

функция. Вначале изучим вопрос о существовании ограниченных на R решений у уравнения (2.21). Сформулируем ряд 

условий относительно функции f(t,x): существуют такие числа a и b (a≤b), C_a и C_b что 

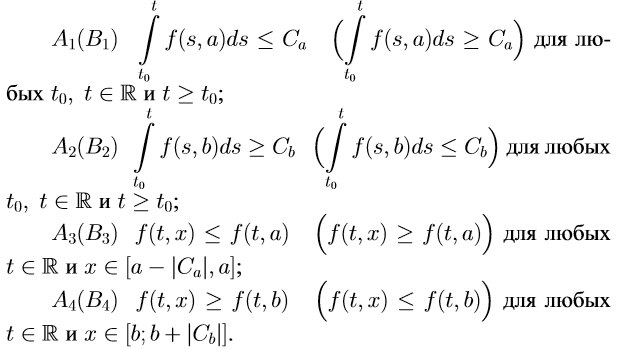
             Заметим, что если C_a=0 (C_b=0), то условия A₃,B₃ (A₄,B₄) выполнены для f(t,x). Справедливо следующее 

утверждение.

             Теорема 2.15. Пусть функция f(t,x) удовлетворяет условиям A₁−A₄ или B₁−B₄. Тогда уравнение (2.21) имеет по 

крайней мере одно ограниченное на R решение, значения которого принадлежат отрезку [a−|C_a|,b+|C_b|]. 

Доказательство.

              Замечание. Если a=b и C_a=C_b=0, то f(t,a)=0, и в этом случае x(t)≡a — ограниченное решение. Если в уравнении 

(2.21) функция f(t,x) монотонна по x, то одна из пар условий (A₃, A₄), (B₃, B₄) выполняется при любых a и b. В этом случае 

имеет место следующее утверждение. 

              Теорема 2.16. Пусть f(t,x) при каждом t возрастает по x (при каждом t убывает по x). Тогда для того, чтобы 

уравнение (2.21) имело ограниченное на R решение, необходимо и достаточно, чтобы функция f(t,x) удовлетворяла 

условиям A₁−A₂ (B₁−B₂). 

Доказательство. 

              Перейдем теперь к изучению нелинейного дифференциального уравнения (2.21) в случае, когда функция f(t,x) 

является периодической по t. Всюду далее уравнение (2.21) будет изучаться при следующих предположениях относительно 

f(t,x):

   C: существует такое число ω>0, что f(t+ω,x)=f(t,x), t∈R;

   D: функция f(t,x) при каждом t возрастает (при каждом t убывает) по x. Имеет место следующая теорема. 

              Теорема 2.17. Пусть функция f(t,x) удовлетворяет условиям C и D. Для того, чтобы уравнение (2.21) имело 

ограниченное на R решение, необходимо и достаточно, чтобы существовало такое x₀, что

Доказательство. 

             Исследуем теперь вопросы периодичности и устойчивости ограниченных решений уравнения (2.21). Справедлива 

следующая лемма.

             Лемма 2.5. Пусть функция f(t,x) непрерывна и при каждом t∈R убывает по x. Тогда все решения уравнения (2.21) 

бесконечно продолжимы вправо, и для любых двух решений x(t) и y(t) функция r(t)=|x(t)−y(t)| убывает. Пусть функция f(t,x) 

непрерывна и при каждом t∈R возрастает по x. Тогда все решения уравнения (2.21) бесконечно продолжимы влево, и для 

любых двух решений x(t) и y(t) функция r(t)=|x(t)−y(t)| возрастает. 

Доказательство.

             Замечание. Из леммы 2.5 следует, что если функция f(t,x) возрастает по x, то задача Коши x'(t)=f(t,x(t)), x(t₀)=x₀, 

t ≤ t₀ имеет единственное решение. Если же функция f(t,x) убывает по x, то единственное решение имеет задача 

Коши вида x'(t)=f(t,x(t)), x(t₀)=x₀, t ≥ t₀. 

             Докажем следующее утверждение. 

             Лемма 2.6. Пусть функция f(t,x) удовлетворяет условиям C и D. Если уравнение (2.21) имеет два различных 

определенных на R ограниченных решения x(t) и y(t), значения которых принадлежат отрезку [α,β], то оно имеет 

бесконечное семейство определенных на R решений вида {z(t)+c}, c∈[0,c₀] (c₀>0), значения которых принадлежат отрезку 

[α,β]. 

Доказательство.

             Имеет место теорема.

             Теорема 2.18. Пусть функция f(t,x) удовлетворяет условиям C и D. Тогда все ограниченные решения уравнения 

(2.21) являются периодическими с периодом ω.

Доказательство.

             Следствие. Если f(t,x) удовлетворяет условиям C и D и уравнение (2.21) имеет ограниченное (ω-периодическое) 

решение, то существует такой промежуток <α,β> вида: [α,β], (−∞,β], [α,+∞), (−∞,+∞), что семейство функций {x(t)+c}, 

c∈<α,β>, совпадает с множеством всех ω-периодических (ограниченных) решений уравнения (2.21). 

Доказательство. 

             Исследуем теперь вопросы единственности и устойчивости ω-периодического решений уравнения (2.21). 

             Непосредственно из леммы 2.5 вытекает следующий результат.

             Теорема 2.19. Пусть функция f(t,x) удовлетворяет условию C и при каждом t∈R функция f(t,x) убывает по x. Тогда 

все решения уравнения (2.21) устойчивы.

             Теорема 2.20. Пусть функция f(t,x) удовлетворяет условиям C и D и при некотором t₁ функция f(t₁,x) строго 

монотонна. Тогда уравнение (2.21) имеет единственное ωпериодическое (ограниченное) решение. Если при этом f(t,x) 

убывает по x, то ω-периодическое (ограниченное) решение будет равномерно асимптотически устойчиво в целом.

Доказательство.