Учебная практика

             Исследуем вопросы существования ограниченных и периодических решений нелинейных дифференциальных 

систем с периодической правой частью. Рассмотрим нелинейную систему дифференциальных уравнений x'(t)=f(t,x), (2.15) 

где f : R^m+1→R^m —непрерывная функция, удовлетворяющая условию: существует ω>0, такое что f(t+ω,x)=f(t,x). (2.16) 

             Докажем следующие очевидные утверждения. 

             Лемма 2.2. Пусть функция f(t,x) непрерывна и удовлетворяет условию (2.16). Тогда она ограничена в любой полосе 

D={(t,x) : t∈R, x∈[−k,k]}. 

Доказательство.

             Лемма 2.3. Пусть функция x(t) является решением системы (2.15). Тогда функция x(t+ω) также является решением 

этой системы. 

Доказательство. 

             Лемма 2.4. Пусть последовательность дифференцируемых функций {x_n(t)}, x : R→Rm, удовлетворяет условиям

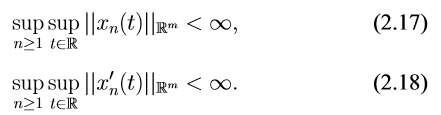
             Тогда из нее можно извлечь подпоследовательность, сходящуюся равномерно на каждом отрезке. 

Доказательство. 

             Теорема 2.9. Пусть система (2.15) имеет решение x(t), определенное и ограниченное на полуоси [a,∞). Тогда эта 

система имеет решение y(t), определенное и ограниченное на R, причем для каждого t∈R 

Доказательство.

              Следствие. Если система имеет решение x(t), такое, чтото функция y(t)≡a, t∈R, 

является решением этой системы. 

              Теорема 2.10. Пусть система (2.15) имеет решение x(t), удовлетворяющее для некоторого a∈R условию 

x(a+ω)=x(a). Тогда она имеет ω-периодическое решение, определенное на R. 

Доказательство.

              Замечание. Если через каждую точку пространства R^m+1 проходит единственная интегральная кривая системы 

(2.15),то решение, удовлетворяющее условию x(a)=x(a+ω), продолжимо на всю ось и является ω-периодическим. Если 

система не удовлетворяет условиям единственности решения, то, вообще говоря, система может иметь решение, 

определенное на R, удовлетворяющее условию x(a)=x(a+ω), но не являющееся ω-периодическим. 

              Теорема 2.11. Пусть система (2.15) имеет решение x(t), определенное и ограниченное на [a,+∞), принимающее 

значения в некотором компакте B⊂R^m. Пусть, кроме того, система не имеет других решений y(t), таких что y(t)∈B для всех 

t∈[a,+∞). Тогда система (2.15) имеет ω-периодическое решение, определенное на R.

Доказательство.

              Теорема 2.12. Пусть через каждую точку пространства R^m+1 проходит единственная интегральная кривая системы 

(2.15) и пусть система (2.15) имеет единственное определенное и ограниченное на [a,+∞) (или (−∞,a]) решение x(t). Тогда 

это решение продолжимо на R и является ω-периодическим.

Доказательство.

              Замечание. Теоремы 2.9, 2.11, 2.12 остаются справедливыми при замене промежутка [a,+∞) промежутком (−∞,a]. 

              Теорема 2.13. Пусть система (2.15) имеет решение x(t), определенное и ограниченное на R, и принимающее 

значения в некотором компакте B⊂R^m. Пусть, кроме того, система не имеет других решений y(t), таких что y(t)∈B для всех 

t∈R. Тогда решение x(t) является ω-периодическим. 

Доказательство.

              Теорема 2.14. (Массера). Пусть уравнение (2.15) удовлетворяет условиям единственности решения и имеет 

решение, определенное и ограниченное на [a,+∞) (или (−∞,a]). Тогда уравнение (2.15) имеет ω-периодическое решение.

Доказательство.