Учебная практика

             Вернемся к вопросу о периодичности суммы и произведения периодических функций. В утверждении 1.1 

рассмотрен случай, когда функции f(t), g(t) имеют одинаковые периоды. Выясним, сохранится ли свойство периодичности 

суммы и произведения для произвольной пары периодических функций. 

             Действительные числа a и b называются соизмеримыми, если существуют такие целые числа p и q, что ap+bq=0. 

             Если одно из чисел a,b равно нулю (пусть для определенности, a=0), то числа a и b, очевидно, соизмеримы. Для 

доказательства достаточно положить p=1, q=0. Пусть a$\neq$0, рассмотрим отношение 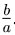. Числа a и b соизмеримы тогда и 

только тогда, когда 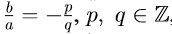, т. е. отношение  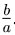есть рациональное число. Таким образом, два действительных 

числа соизмеримы тогда и только тогда, когда либо одно из них равно нулю, либо их отношение есть рациональное число.

             Теорема 1.4. Пусть периодические функции f(t) и g(t) имеют отличные от нуля соизмеримые периоды. Тогда 

функции f(t)+g(t) и f(t)g(t) являются периодическими.

Доказательство.

             Для рассмотрения случая, когда периоды функций f(t) и g(t) несоизмеримы, докажем предварительно 

вспомогательное утверждение. С учетом его дальнейших приложений, оно доказывается в более общей форме, чем нам 

потребуется.

             Лемма 1.1. Пусть числа a и b не являются соизмеримыми. Тогда для любого ξ∈R найдутся такие сходящиеся к ξ 

последовательности {n_ka+m_kb} и {p_ka+d_kb}, где n_k, m_k, p_k и d_k — целые числа, что выполняются следующие условия. 

1. Если числа a и b одного знака, то последовательности {n_k} и {d_k} стремятся к +∞, а {m_k} и {p_k} — к −∞. 

2. Если числа a и b разных знаков, то последовательности {n_k} и {m_k} стремятся к +∞, а {p_k} и {d_k} — к −∞. 

Доказательство.

             Теорема 1.5. Пусть f(t), g(t) — периодические функции, причем множество точек разрыва одной из них имеет 

нулевую меру Лебега. Если все отличные от нуля периоды функций f(t) и g(t) попарно несоизмеримы, то функция f(t)+g(t) 

не является периодической. 

Доказательство.

             Замечание. Нетрудно видеть, что теорема остается справедливой, если вместо равенства нулю меры Лебега 

множества точек разрыва одной из функций потребовать, чтобы одна из функций была непрерывна на интервале сколь 

угодно малой длины. 

             Теорема 1.6. Пусть f(t), g(t) — периодические функции, причем найдутся такие точки t₀ и t₁, в которых обе функции 

непрерывны, f(t₀)$\neq$0, g(t₀)$\neq$0 и f(t₁)$\neq$f(t₀), g(t₁)$\neq$g(t₀) и множество точек разрыва одной из них имеет нулевую меру 

Лебега. Если наименьшие положительные периоды функций f(t) и g(t) несоизмеримы, то функция f(t)g(t) не является 

периодической. 

Доказательство.

               Замечание. Если условия теоремы не выполнены, то произведение двух периодических функций может быть 

периодической функцией и в том случае, когда их наименьшие положительные периоды несоизмеримы. Примером может 

служить пара функций