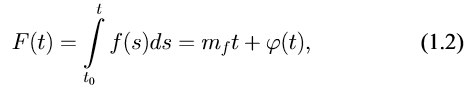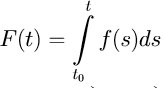Учебная практика

            Теорема 1.7. Если ω-периодическая функция f(t) дифференцируема на R, то ее производная также является 

ω-периодической функцией. 

Доказательство. 

            Всюду ниже в этом параграфе будем считать, что функция f(t) интегрируема по Риману на каждом отрезке из R, 

интеграл понимается как интеграл Римана. Так как интегрируемая по Риману функция не может быть разрывна в каждой 

точке R, то в силу следствия 1.3 функция f(t) либо имеет наименьший положительный период, либо f(t) ≡ const. Ниже 

ω—произвольный, не обязательно наименьший, положительный период функции f(t). 

            Утверждение 1.9. Пусть f(t) — периодическая функция периода ω. Тогда для произвольного числа a∈R выполнено 

равенство 

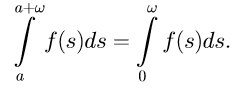
Доказательство.

           Определение 1.6. Величина

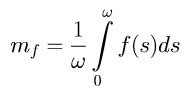
называется средним значением ω-периодической функции f(t). Легко видеть, что среднее значение периодической функции 

f(t) не зависит от выбора ее периода ω.

             Теорема 1.8. Пусть f(t) — ω-периодическая функция. Тогда ее интеграл имеет вид

где m_f — среднее значение функции f(t), а ϕ(t) — непрерывная на R ω-периодическая функция. 

Доказательство. 

              Следствие 1.4. Пусть f(t)—ω-периодическая функция.

Интеграл  является периодической функцией

тогда и только тогда,когда среднее значение m_f функции f(t) равно нулю. При этом ω является периодом функции F(t). 

Доказательство. 

              Следствие 1.5. Пусть f(t) — ω-периодическая функция.

Интеграл   ограничен тогда и только тогда,

когда среднее значение mf функции f(t) равно нулю. 

Доказательство.

              Суммируя полученные результаты, получаем следующее утверждение.

              Теорема 1.9. Пусть f(t) — ω-периодическая функция. Следующие утверждения эквивалентны:

1) интеграл   ограничен;

2) интеграл   есть функция периодическая;

3) среднее значение функции f(t) равно нулю.